今年も様々な方に有形無形を問わずお世話になりました。感謝の気持ちを込めて大晦日に多少長めの記事を書いてみました。よろしければごらんください。
課題の提示
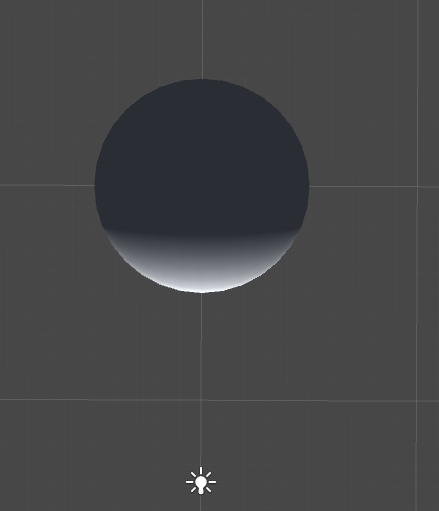
まず、こちらの画像をご覧ください。

シーンに球体とポイントライトを一個配置しています。ディレクショナルライトは削除してあるので、ポイントライトに照らされている所のみに色がついています。
ポイントライトを動かすと以下のように色がつく(=光が当たる)場所が変わります。


このの描画を実現する為の最低限のシェーダーコードは以下になります。
Shader "Unlit/NewUnlitShader"
{
SubShader
{
Pass
{
Tags { "LightMode" = "ForwardAdd" }
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct v2f
{
float4 vertex : SV_POSITION; //プロジェクション空間座標
float4 diffuse :COLOR0; //色
};
//頂点シェーダー
//vertext:頂点のモデル空間座標
//normal:頂点のモデル空間法線ベクトル
v2f vert (float4 vertex : POSITION, float4 normal : NORMAL)
{
v2f Out;
//頂点座標をプロジェクション空間へ変換する
Out.vertex = UnityObjectToClipPos(vertex);
//モデル空間でのライトの方向ベクトルを取得し、単位ベクトル化して格納する
float3 LightDir= normalize(ObjSpaceLightDir(vertex));
//描画色(白)
float4 Color = float4(1, 1, 1, 0);
//法線ベクトルとライト方向との内積を取り(0未満なら0)、色と乗算する
Out.diffuse = Color * max(0, dot(normal, LightDir));
return Out;
}
//フラグメントシェーダー
fixed4 frag (v2f In) : SV_Target
{
//ラスタライザが補間した色の値をそのまま返す
return In.diffuse;
}
ENDCG
}
}
}シェーダーコードの読み方については解説しません。ShaderLab&HLSLについて詳しく知りたい方は土屋のシェーダー本(https://s-games.booth.pm/items/660001)をよければどうぞ)。
今回はこのコードの中のこの1行について取り上げます。
//法線ベクトルとライト方向との内積を取り(0未満なら0)、色と乗算する Out.diffuse = Color * max(0, dot(normal, LightDir));
シェーダーのサンプルコードを読んでいると、よくこんな感じのコードに出会います。
ここでのnormalは頂点が持つ法線ベクトル、LightDirは頂点から光源座標へのベクトルが代入されています。どちらもモデル空間座標で、正規化された単位ベクトルです。
HLSLのリファレンスからmaxやdotの関数の機能をピックアップすると、maxは2つの入力のうち大きい方を返し、dotは2つのベクトルの内積を返す関数だとわかります。なので、このコードは「頂点の法線ベクトルと光源方向ベクトルの内積を取り(ただし結果が0未満の場合は0)、その値を拡散率として描画色に乗算する」という処理になります。
拡散率は0.0から1.0までの値を取るので、これを描画色に乗算することによって、「光源方向に対して面が垂直になっている(=面を向けている)ほど白く、角度がつくほど黒く描画する」という事を実現しています。実際の画面を見ると、実際そうなっているのがわかります(※1)。
ところが、なんで法線ベクトルと光源方向ベクトルの内積を取ると拡散率が算出されるのか。これが分からないw
プログラミングに詳しくない方は意外に思われるかもしれませんが、土屋は数学が苦手なタイプのエンジニアでして、高校時代の数学の時間はほぼ寝て過ごしました。なので、シェーダープログラミングの勉強中にちょくちょく出てくる「ベクトルの内積」が、どういう性質を持つ物なのかが良く分からず、ググッてみてもいまいちピンとくる物がありませんでした。
今回は、この「どうして法線ベクトルと光源方向ベクトルの内積を取ると拡散率を算出できるのか」について、解説してみたいと思います。
【注記】上記のような理由で、土屋は数学に明るくなく、以下の解説も重要な要素が抜け落ちてたり、そもそも説明が間違ってたりする所があるかもしれません。その際はどうぞコメントにてご指摘ください。みなさんのコメントを合わせることで、記事の完成度を上げられればと思います。
※1
注意:今回は光源からの距離については無視していて、あくまで光源に対する面の角度のみに注目しています
光と面のなす角度
通常、ポリゴンの表面の色を決める時には、その表面が光源に対してどのような角度を向いているかが重要になります(※1)。なぜ光源に対する角度が重要なのかと言いますと、光というのは物体表面に対して直行している時に最も反射し、角度が開いていくごとに反射率が落ちるという性質があるからです。

上図は先ほどと同じ画像です。球体の表面のうち、ライトの位置に直行している部分が一番明るく、そこから外れるとどんどん暗くなるのが分かります。

これはライトの方向から球体を見た物。ライトによって明るくなっているのが、球体の半分よりも狭い範囲であることに注目してください。ライトと角度が0度よりも大きくなった場合、もう光は反射しません(そりゃそうだ)。

ライトを球体にぐっと近づけました。さっきよりも明るい範囲が小さくなっていますね。ライトの効果を受ける範囲が、サーフェスとの角度に依存していることがよくわかります。

よりわかりやすくするために、見た目をローポリ化してみました(※2)。これだと、面の角度によって色が変化しているのが一目瞭然ですね。
※1
実際にはカメラとの角度も重要なのですが、煩雑になるので今回の記事では省略します
※2
実際には、法線ベクトルの向きをリセットしただけで、使っているポリゴンモデルは同じものです。
角度を算出する方法。
さて、サーフェスの色を決める時にサーフェスとライトがなす角度、より正確には「ライトが表面にどれだけ直行しているか」が重要であることがわかりました。逆に言えば、「ライトが表面にどれだけ直行しているか」がわかれば、描画色をどれくらい暗くすれば良いかがわかるわけです。しかし、それって、どうやって算出すればいいんでしょうか?
シェーダープログラミングというのは恐ろしく泥臭い作業でして、乱暴に言えば、全てのポリゴンの表面1ドットごとにシェーダーコードと呼ばれるプログラミングを実行し、その演算を合算することで、1フレーム分の画像を生成しています。想像するだに物凄い計算量ですが、実際にはその1ドットごとに何十回も異なる演算をすることになるので、毎フレームの計算量は膨大な物になります。
そのため、シェーダープログラミングではシェーダーの処理負荷を下げるために、「しなくていい計算は可能な限りしない」が基本方針になります。
2つのベクトルをなす角度を計算するのはそこまで難しい作業ではないでしょう(多分。知らない)。しかし、その演算量は可能な限り少なくしたい。そこで登場するのが内積なのです(ふう、やっと出てきたぞ!)。
ベクトルの内積
まず、ベクトルの内積というのは下記のようにベクトルの各成分を乗算した上で、その全てを足し合わせる計算の事を言います(以下、3次元ベクトルの場合に限定します)。
a・b = a.x * b.x + a.y * b.y + a.z * b.z; ……①
ベクトルの内積は「a・b」のように、2つのベクトルをドットで繋いで表記します。その為、海外では「ドット積」と呼ばれる事が多いようです。HLSLでも、内積の組み込み関数はdotという名前になっています。
さて、上で説明したように、ベクトルの内積は、各成分を乗算して足し合わせた「だけ」の物です。この単純な計算が一体なんの役に立つんでしょうか? これ、正直土屋にもよくわかりません(爆)。ところが、ベクトルの内積の性質を利用すると、この単純な計算で、我々が今必要としている情報を得ることができるのです。
まず内積の性質から。ベクトルの内積は、下記の式からも算出できます。
a・b = ||a|| ||b||cosθ; ……②
aとbそれぞれの長さと、2つのベクトルが作る角度θのコサインを掛けると、①と同じ結果が出せます(①と②が同じ結果を返す証明については、ネットでググれば沢山出てくるので省略します)。
さて、シェーダーで内積を取る時に使用する法線ベクトルやライト方向ベクトルは、正規化されたベクトルです(そうで無いときは、あらかじめ正規化する必要があります)。ベクトルは正規化すると単位ベクトルになります。単位ベクトルとは、長さが1のベクトルです。長さが1のベクトル2つの内積を、先ほどの②の式に当てはめてみます。
||a|| ||b||cosθ ……② = 1 * 1 * cosθ = cosθ
おわかりのように、正規化されたベクトル同士の内積を取ると、その結果はcosθになります。そして、①と②は同じ結果になるので、①を使って法線ベクトルとライト方向ベクトルの各要素を乗算し足し合わせると、それは②の結果、すなわち、法線ベクトルとライト方向ベクトルのcosθになるというわけです。どうですか、面白いでしょ!?(驚きの押し売り)
cosθはなんなのか。
さて、算出できたのはいいけれど、この「cosθ」とはどんな値を取るのでしょうか。高校時代に習った記憶があるでしょうが、cosθは角度に応じて以下のような値を取ります。
0°= 1 90°= 0 180°=-1 270°= 0 360°= 1
この場合のθは、法線ベクトルとライト方向ベクトルがなす角です。この角度が0ということは、法線ベクトルとライト方向ベクトルが同じ、つまり、ポリゴンの面が完全にライトの方向に向いているという事になります。この時cosθは1になります。そして、角度が徐々に開いていくに従ってcosθの値は0に近づいていき、90度になった時点で0になります(90度より開いた場合にはマイナスになりますが、シェーダーコードではmax関数を使って0未満はすべて0としています)。
前述した通り、シェーダーでプリミティブ平面の色を決める時には「その平面がライトに対してどれくらいの角度になっているか」が重要になりますが、その角度を算出するのは非常に面倒です。しかし、法線ベクトルとライト方向ベクトルの内積(=ベクトル同士の各成分を乗算して足し合わせるという非常にコストの低い処理)を計算するだけで、プリミティブ平面がライト方向に向いている割合を算出出来るので、非常に重宝するのです。
終わりに
学生時代、数学が人生の役に立たないとは思いませんでしたが、社会人になったら一生使うことはないだろうと正直思っていました。けれど、シェーダープログラミングを習得する(それはつまり、AAAタイトルのグラフィックエンジニアを目指すと同義です)には、ベクトルの内積はもちろん、行列とベクトルの乗算、様々な物理現象近似式など、多くの数学的知識を習得する必要があります。
土屋のように高校の数学の時間を寝て過ごしている学生がこれを読んでいたら、せめてベクトルと行列まではちゃんと勉強しておこう。そうじゃないと、今の土屋みたいに、大人になってから凄く苦労しますよw。